19 Nov
Productos notables
Productos notables es el nombre que reciben multiplicaciones con expresiones algebraicas cuyo resultado se puede escribir mediante simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.
Factor común
El resultado de multiplicar un binomio a+b por un término c se obtiene aplicando la propiedad distributiva:
c (a + b) = c a + c b
Para esta operación existe una interpretación geométrica, ilustrada en la figura adjunta. El área del rectángulo es c (a + b) (el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas: ca y cb.
Ejemplo: 3x (4x + 6y) = 12x^2 + 18xy
Binomio al cuadrado o cuadrado de un binomio
Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Así:
(a + b)^2 = a^2 + 2 a b + b^2
Un trinomio de la expresión siguiente: a^2 + 2 a b + b^2; se conoce como trinomio cuadrado perfecto.
Cuando el segundo término es negativo, la ecuación que se obtiene es:
(a – b)^2 = a^2 – 2 a b + b^2
En ambos casos el signo del tercer término es siempre positivo.
Ejemplo: (2x – 3y)^2 = 4x^2 -12xy +9y^2
Producto de dos binomios con un término común
Cuando se multiplican dos binomios que tienen un término común, el cuadrado del término común se suma con el producto del término común por la suma de los otros, y al resultado se añade el producto de los términos diferentes.
(x+a)(x+b)= x^2+(a+b)x+ab
Ejemplo: (3x+4)(3x-7) = 9x^2 -9x -28
Producto de dos binomios conjugados
Dos binomios conjugados se diferencian sólo en el signo de la operación. Para su multiplicación basta elevar los monomios al cuadrado y restarlos (obviamente, un término conserva el signo negativo), con lo cual se obtiene una diferencia de cuadrados.
(a + b)(a – b) = a^2 – b^2
Ejemplo: (3x+5y)(3x-5y) = 9x^2 – 25y^2
Polinomio al cuadrado
Para elevar un polinomio de cualquier cantidad de términos se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.
(a+b+c)^2 = a^2 +b^2+c^2 + 2(ab+ac+bc)
(a+b+c+d)^2 = a^2 +b^2+c^2 + d^2+ 2(ab+ac+ad+bc+bd+cd)
Ejemplo: (3x+2y-5z)^2 = 9x^2+4y^2+25z^2 +12xy-30xz-20yz
Binomio al cubo
Para calcular el cubo de un binomio se suman, sucesivamente:
El cubo del primer término con el triple producto del cuadrado del primero por el segundo.
El triple producto del primero por el cuadrado del segundo.
El cubo del segundo término.
(a+b)^3= a^3+3a^2b+3ab^2+b^3
Ejemplo: (x+2y)^3 = x^3+6x^2y+12xy^2+8y^3
Si la operación del binomio implica resta, el resultado es:
El cubo del primer término.
Menos el triple producto del cuadrado del primero por el segundo.
Más el triple producto del primero por el cuadrado del segundo.
Menos el cubo del segundo término.
(a-b)^3= a^3-3a^2b+3ab^2-b^3
Factorización
Factorizar una expresión algebraica (o suma de términos algebraicos), es el procedimiento que permite escribir como multiplicación dicha expresión.
Los factores o divisores de una expresión algebraica, son los términos, ya sean números y/o letras, que multiplicados entre sí dan como producto la primera expresión.
Así, por ejemplo, si multiplicamos a por a + b podemos ver qué;

Dan como producto a^2 + ab, entonces, los factores o divisores de esta expresión algebraica son a y a + b.
Métodos utilizados para factorizar un polinomio.
Primero debes saber que, no todos los polinomios se pueden factorizar, ya que, al igual que en los números primos que sólo son divisibles por ellos mismos y por 1, hay expresiones algebraicas que también solo son divisibles por ellas mismas y por 1.
Por ejemplo, el polinomio ax + by + cz, no se puede factorizar ya que, solo es divisible por ax + by + cz y por 1. Es decir, este polinomio no tiene un factor en común.
Para poder factorizar una expresión algebraica es necesario que siempre exista al menos un factor en común dentro de sus términos, ya sean números y/o letras.
Factor común de una expresión algebraica es el máximo común divisor (m.c.d.) de los términos que la componen.
Factor común monomio.
Debes identificar el factor común entre todos los términos de la expresión, y escribirlo como coeficiente de un paréntesis, en el cual tienes que escribir los términos resultantes después de dividir por el factor común.
Ejemplos;
a) Factorizar x^2y + x^2z.
Identificamos el factor común de x^2y y x^2z el cual es x^2, entonces dividimos los términos de la expresión por x^2; x^2y : x^2 = y y x^2z : x^2 = z. Ahora escribimos la factorización;
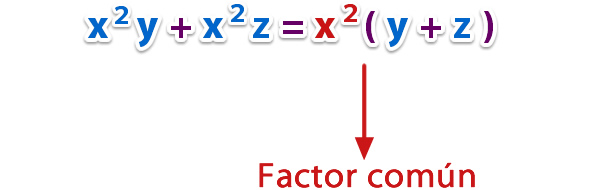
b) Factorizar 8 m^2 – 12 mn.
Identificamos el factor común de 8 m^2 y 12 mn el cual es 4m, entonces dividimos los términos de la expresión por 4m; 8 m^2 : 4m = 2m y 12 mn : 4m = 3n. Ahora escribimos la factorización;

Lenguaje algebraico
El lenguaje algebraico es una forma de traducir a símbolos y números lo que normalmente tomamos como expresiones particulares. De esta forma se pueden manipular cantidades desconocidas con símbolos fáciles de escribir lo que permite simplificar teoremas, formular ecuaciones e inecuaciones y el estudio de cómo resolverlas. Este lenguaje nos ayuda a resolver problemas matemáticos mostrando generalidades. EL lenguaje algebraico nace en la civilización musulmana en el periodo de AL-Khwarizimi durante la edad media. Su función principal es establecer y estructurar un idioma que ayuda a generalizar las distintas operaciones que se desarrollen dentro de la aritmética donde solo ocurren los números y sus operaciones aritméticas elementales (+ -x %).
Una expresión algebraica es una cadena de representaciones perteneciente al lenguaje algebraico, el cual puede contener variables, números, así como también operaciones aritméticas. El Término, es una expresión algebraica donde hay solo operaciones de multiplicación y división de letras y números, tanto el numero como la letra puede estar elevado a una potencia. El termino independiente solo consta de un valor numérico, en tanto los términos semejantes son los que tienen debidamente la misma parte de letras (parte literal) y varían solo su coeficiente. Estos solo se pueden sumar y restar, si los términos no son semejantes ya no es posible, lo que si es posible es dividir o multiplicar todo tipo de termino. El grado de un término puede ser de grado absoluto, lo cual es la suma de los exponentes de cada letra, o puede ser un término de grado relativo en lo cual se toma en cuenta la letra y su exponente.
Los signos de agrupaciones se usan para cambiar el orden de las operaciones, se indica dentro de estos cual de las operaciones debe realizarse en primer lugar, estos símbolos son el paréntesis (), el corchete [], y la llave {}. Se utilizan también signos de relación tales como <, menor que; > mayor que; y =; igual a. El lenguaje algebraico se constituye principalmente de las letras del alfabeto del cual las primeras letras por lo general son las que determinan valores conocidos o datos del problema, (aunque se puede utilizar cualquier letra del alfabeto). Se utilizan también algunos vocablos griegos. En general las letras X; Y y Z se utilizan como las incógnitas o variables de la expresión algebraica.
Los siguientes son ejemplos de las expresiones algebraicas mas usadas, en forma verbal y escrita:
La suma de dos números
a + b
La resta o diferencia de dos números
X – y
El producto de dos números
ab
El cociente de dos números
X/y
El cociente de la suma de dos números, sobre la diferencia
a+b/a-b
El doble de un número
2X
El doble de la suma de dos números
2(a+b)
El triple de la diferencia de dos números
3(x-y)
La mitad de un número
X/2
La mitad de la diferencia de dos números
(x-4)/2
El cuadrado de un número
El cuadrado de la suma de dos números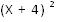
El triple del cuadrado de la suma de dos números.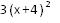
La suma de 3 números
A+b+c
La semi suma de dos números.
(a+b)/2
Fracciones
Algunas de las operaciones básicas que se pueden realizar con las fracciones son las siguientes:
| Suma o Resta | a/b ± d/c = (a⋅c ± b⋅d)/b⋅c |
| Producto | a/b ⋅ b/c = a⋅b/b⋅c |
| División | a/b ÷ c/d = a⋅d/b⋅c |

Deja un comentario